» k-fold thesIt

Latest Updates: k-fold RSS

Arif 12:41:37 pm on August 22, 2010 | 0 | # |
Tags: cross-validation, error, estimation, k-fold, Michaelsen 1987, reference, Stone 1974

Stone 1974 is referenced in:
Michaelsen J. 1987. Cross-validation in statistical climate forecast models. J Climate Applied Meteorology, 26:1589-1600

1520-0450(1987)026-1589-cviscf-2.0.co;2.pdf

Set 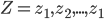$Z = z_{1}, z_{2},... , z_{1}$ consists of predictions and targets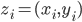 $z_{i}=(x_{i}, y_{i})$

A set of prediction rule 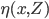$\eta (x,Z)$ will be used to predict y₀ from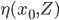 $\eta (x_{0},Z)$

Let 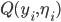$Q(y_{i},\eta_{i})$ be the accuracy.
by least squares this will usually 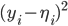$(y_{i}-\eta_{i})^{2}$
in other words expected Err is
$Err= E[Q(y_{i},\eta(x_{0},Z))]$

MSE

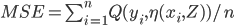
$MSE= \sum_{i=1}^{n}Q(y_{i},\eta(x_{i},Z))/n$

In cross validation
$MSE_{(CV)}= \sum_{i=1}^{n}Q(y_{i},\eta(x_{i},Z_{(i)}))/n$
Arif 06:29:08 pm on August 21, 2010 | 0 | # |
Tags: cross-validation, Fu 1994, k-fold, validation

../sT-fold cross-validation (Stone 1974) repeats k times for a sample set randomly divided into k disjoint subsets, each time leaving one set out for testing and the others for training. Thus, we may call this technique “leave some out”