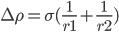Interfacial tension and centrifugal forces balanced at mechanical equilibrium.
centrifugal-IFT equilibrium
Interfacial tension of any liquid that gives a shape very close to a cylinder at the equilibrium point, can be estimated using Vonnegut’s expression:
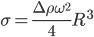
ω : angular velocity; (radians per second, degrees per second, revolutions per second)
Δρ : difference between two fluid: the less-dense and the dense
Escobedo and Mansoori (AIChE J. 42(5): 1425, 1996) Found original paper: check Escobedo 1996
The proposed 1996 paper relates the surface tension of mixtures to bulk-phase concentrations and properties (i.e. densities). Surface tension of pure organic fluids σ:
![\sigma=[P(\rho_l-\rho_v)^4]](http://lakm.us/thesit/wp-content/uploads/eq_90c5333f1eb13eb375ab39bad2a55fd3.png)
The two ρ are densities: liquid and vapour.
They introduced parachor (P), a new expression, derived from statistical mechanics (from Macleod equation) which represents the experimental surface tension of 94 different organic compounds within 1.05 AAD% (average absolute deviations).
(Kumar 2005) It expresses the surface tension of a liquid in equilibrium with its own vapour. Historical reference for parachor cited here: Macleod, Sugden, Quayle, Escobedo.
Young Laplace equation:
other uses γ instead of σ for surface/interfacial tension (i.e. Pashley 2004). Common unit is dyne/cm (1 dyne = 1 micro Newton (μN) ).