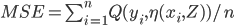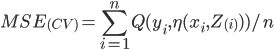Feedforward Neural Network Construction Using Cross Validation. Rudy Setiono. Neural Computation 13(12): 2865-2877.
This article presents an algorithm that constructs feedforward neural networks with a single hidden layer for pattern classification. The algorithm starts with a small number of hidden units in the network and adds more hidden units as needed to improve the network’s predictive accuracy. To determine when to stop adding new hidden units, the algorithm makes use of a subset of the available training samples for cross validation. New hidden units are added to the network only if they improve the classification accuracy of the network on the training samples and on the cross-validation samples.
Extensive experimental results show that the algorithm is effective in obtaining networks with predictive accuracy rates that are better than those obtained by state-of-the-art decision tree methods.
10.1.1.112.9536.pdf
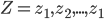 consists of predictions and targets
consists of predictions and targets 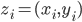
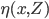 will be used to predict y0 from
will be used to predict y0 from 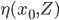
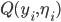 be the accuracy.
be the accuracy.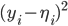
![Err= E[Q(y_{i},\eta(x_{0},Z))]](http://lakm.us/thesit/wp-content/uploads/eq_a3a3253210769351b42ecc2c29b07f59.png)