Approximation Capabilities of Neural Networks. C. Enăchescu, Journal of Numerical Analysis, Industrial and Applied Mathematics (JNAIAM), vol. 3, no. 3-4, 2008, pp. 221-230
From the learning point of view, the approximation of a function is equivalent with the learning problem of a neural network. In this paper we want to show the capabilities of a neural network to approximate arbitrary continuous functions. We have made some experiments in order to confirm the theoretical results.
c48613aed54c29e0f60ca35833aebf70.pdf
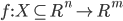 is a continuous function
is a continuous function
Neural Network and Best Approximation Theory
Given 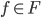 and
and 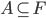 we call the distance of f from A as
we call the distance of f from A as